Binary heap
There are several types of heaps, but in the current article we are going to discuss the binary heap. For short, let's call it just "heap". It is used to implement priority queue ADT and in the heapsort algorithm. Heap is a complete binary tree, which answers to the heap property.
Complete binary tree
It is said, that binary tree is complete, if all its levels, except possibly the deepest, are complete. Thought, incomplete bottom level can't have "holes", which means that it has to be fulfilled from the very left node and up to some node in the middle. See illustrations below.
Correct example of a complete binary tree

Incorrect case, middle level is incomplete
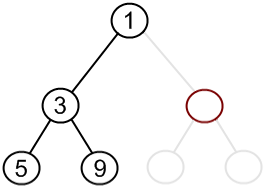
Incorrect case, bottom level has a "hole"
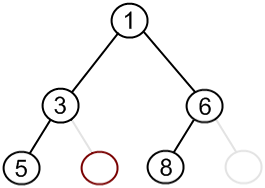
Height of a complete binary tree is O(log n).
Heap property
There are two possible types of binary heaps: max heap and min heap. The difference is that root of a min heap contains minimal element and vice versa. Priority queue is often deal with min heaps, whereas heapsort algorithm, when sorting in ascending order, uses max heap.
Heap property for min heap
For every node in a heap, node's value is lesser or equal, than values of the children.

Heap property for max heap
For every node in a heap, node's value is greater or equal, than values of the children.

To maintain simplicity, in the articles below we consider min-heap only.
See next
- Array-based internal representation
- Inserting an element into a heap
- Removing the minimum from a heap
- Building a heap from an array


|
Contribute to AlgoList
Liked this tutorial? Please, consider making a donation. Contribute to help us keep sharing free knowledge and write new tutorials.
Every dollar helps!