Quicksort
Quicksort is a fast sorting algorithm, which is used not only for educational purposes, but widely applied in practice. On the average, it has O(n log n) complexity, making quicksort suitable for sorting big data volumes. The idea of the algorithm is quite simple and once you realize it, you can write quicksort as fast as bubble sort.
Algorithm
The divide-and-conquer strategy is used in quicksort. Below the recursion step is described:- Choose a pivot value. We take the value of the middle element as pivot value, but it can be any value, which is in range of sorted values, even if it doesn't present in the array.
- Partition. Rearrange elements in such a way, that all elements which are lesser than the pivot go to the left part of the array and all elements greater than the pivot, go to the right part of the array. Values equal to the pivot can stay in any part of the array. Notice, that array may be divided in non-equal parts.
- Sort both parts. Apply quicksort algorithm recursively to the left and the right parts.
Partition algorithm in detail
There are two indices i and j and at the very beginning of the partition algorithm i points to the first element in the array and j points to the last one. Then algorithm moves i forward, until an element with value greater or equal to the pivot is found. Index j is moved backward, until an element with value lesser or equal to the pivot is found. If i ≤ j then they are swapped and i steps to the next position (i + 1), j steps to the previous one (j - 1). Algorithm stops, when i becomes greater than j.
After partition, all values before i-th element are less or equal than the pivot and all values after j-th element are greater or equal to the pivot.
Example. Sort {1, 12, 5, 26, 7, 14, 3, 7, 2} using quicksort.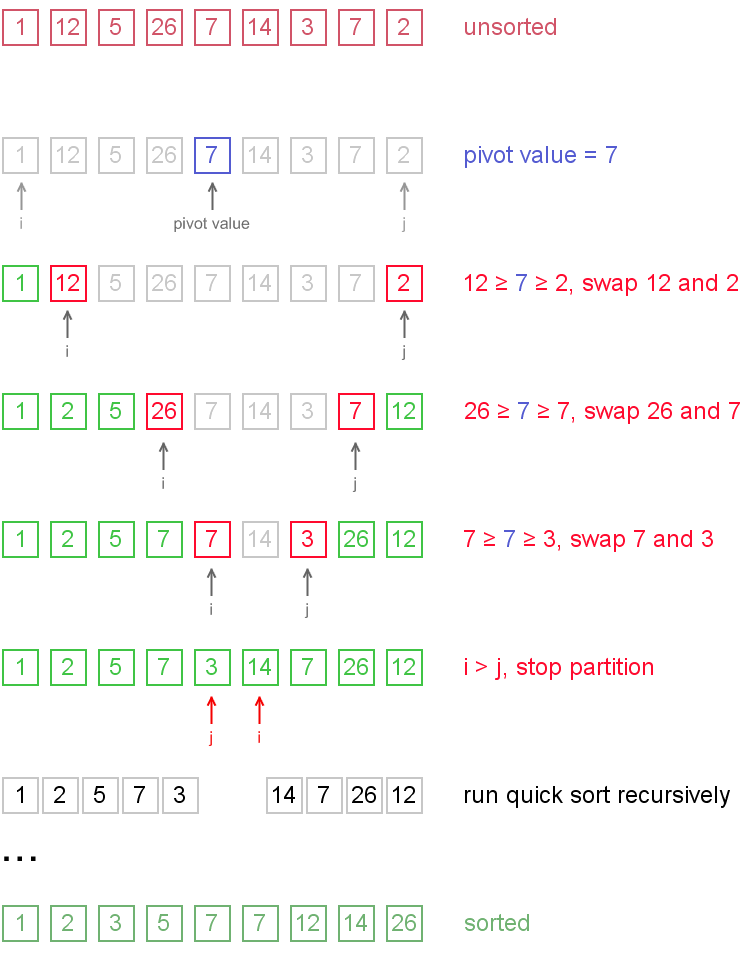
Notice, that we show here only the first recursion step, in order not to make example too long. But, in fact, {1, 2, 5, 7, 3} and {14, 7, 26, 12} are sorted then recursively.
Why does it work?
On the partition step algorithm divides the array into two parts and every element a from the left part is less or equal than every element b from the right part. Also a and b satisfy a ≤ pivot ≤ b inequality. After completion of the recursion calls both of the parts become sorted and, taking into account arguments stated above, the whole array is sorted.Complexity analysis
On the average quicksort has O(n log n) complexity, but strong proof of this fact is not trivial and not presented here. Still, you can find the proof in [1]. In worst case, quicksort runs O(n2) time, but on the most "practical" data it works just fine and outperforms other O(n log n) sorting algorithms.
Code snippets
Partition algorithm is important per se, therefore it may be carried out as a separate function. The code for C++ contains solid function for quicksort, but Java code contains two separate functions for partition and sort, accordingly.
Java
int partition(int arr[], int left, int right)
{
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
while (i <= j) {
while (arr[i] < pivot)
i++;
while (arr[j] > pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
return i;
}
void quickSort(int arr[], int left, int right) {
int index = partition(arr, left, right);
if (left < index - 1)
quickSort(arr, left, index - 1);
if (index < right)
quickSort(arr, index, right);
}
C++
void quickSort(int arr[], int left, int right) {
int i = left, j = right;
int tmp;
int pivot = arr[(left + right) / 2];
/* partition */
while (i <= j) {
while (arr[i] < pivot)
i++;
while (arr[j] > pivot)
j--;
if (i <= j) {
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
};
/* recursion */
if (left < j)
quickSort(arr, left, j);
if (i < right)
quickSort(arr, i, right);
}
Full quicksort package
Full quicksort package includes:- Ready-to-print PDF version of quicksort tutorial.
- Full, thoroughly commented quicksort source code (Java & C++).
- Generic quicksort source code in Java (Advanced).
- Generic quicksort source code using templates in C++ (Advanced).
Recommended books
- Cormen, Leiserson, Rivest. Introduction to algorithms. (Theory)
- Aho, Ullman, Hopcroft. Data Structures and Algorithms. (Theory)
- Robert Lafore. Data Structures and Algorithms in Java. (Practice)
- Mark Allen Weiss. Data Structures and Problem Solving Using C++. (Practice)
Visualizers
- Quicksort Animation (with source code line by line visualization)
- Quicksort in Java Applets Centre
- Animated Sorting Algorithms: Quicksort
Eleven responses to "Quicksort tutorial"
- on Oct 22, 2009 said:
wow this is the BEST explanation i have found yet for quick sort. Thanks!
- on June 19, 2009 said:
very clear and informative. Thanks a lot this was very helpful.
- on April 20, 2009 said:
very good algo for quick sort.............. this helps the student so much
- on Mar 23, 2009 said:
thanks for the tip..it really helps..simple and brief!!^.^..do you have a example flowchart of it?
No, we haven't at the moment. Thought, flowcharts for algorithms is in our to-do-list.
- on Mar 16, 2009 said:
thank you , your codes are really simple to be understood and used
- on Mar 5, 2009 said:
one of the best explanation of quick sort on net. great work. keep it coming!!!!
- on Feb 27, 2009 said:
Thanks for the great program.
it is shorter and simpler than any other quicksort that i have come across. - on Feb 12, 2009 said:
it is really simple and much better than any of the examples i came across..
- on Jan 6, 2009 said:
Thank u i am really happy because the code is simple and can be understood
- on Jan 3, 2009 said:
Really showed exactly what I wanted to know. Now if you could also include something on tail-recursion elimination, it would indeed be very helpful.
We are going to develop "Quick sort in-depth" article, which will examine advanced quick sort problems, such as choosing the pivot value, quick sort optimization on small data volumes, etc.
- on Nov 12, 2008 said:
Thx You :)
Contribute to AlgoList
Liked this tutorial? Please, consider making a donation. Contribute to help us keep sharing free knowledge and write new tutorials.
Every dollar helps!