Removing the minimum from a heap
Removal operation uses the same idea as was used for insertion. Root's value, which is minimal by the heap property, is replaced by the last array's value. Then new value is sifted down, until it takes right position.
Removal algorithm
- Copy the last value in the array to the root;
- Decrease heap's size by 1;
- Sift down root's value. Sifting is done as following:
- if current node has no children, sifting is over;
- if current node has one child: check, if heap property is broken, then swap current node's value and child value; sift down the child;
- if current node has two children: find the smallest of them. If heap property is broken, then swap current node's value and selected child value; sift down the child.
Example
Remove the minimum from a following heap:
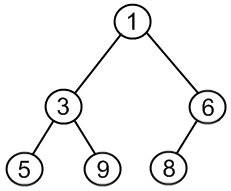
Copy the last value in the array to the root and decrease heap's size by 1:
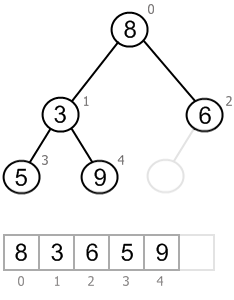
Now heap property is broken at root:
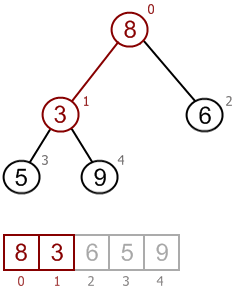
Root has two children. Swap root's value with the smallest:
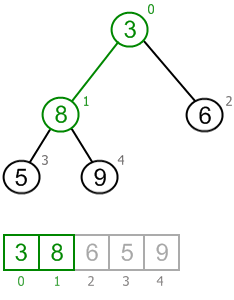
Heap property is broken in node 1:
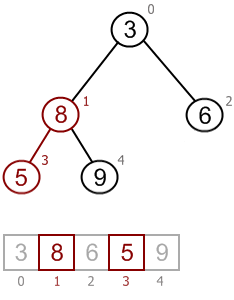
Recover heap property:
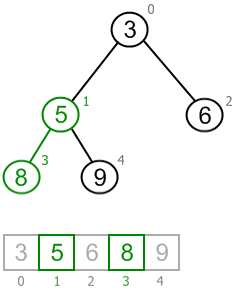
Node 3 has no children. Sifting is complete.
Source heap |
After minimum removal |
 |
 |
Complexity analysis
Complexity of the removal operation is O(h) = O(log n), where h is heap's height, n is number of elements in a heap.
Code snippets
Java implementation
public class BinaryMinHeap {
…
public void removeMin() {
if (isEmpty())
throw new HeapException("Heap is empty");
else {
data[0] = data[heapSize - 1];
heapSize--;
if (heapSize > 0)
siftDown(0);
}
}
…
private void siftDown(int nodeIndex) {
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= heapSize) {
if (leftChildIndex >= heapSize)
return;
else
minIndex = leftChildIndex;
} else {
if (data[leftChildIndex] <= data[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (data[nodeIndex] > data[minIndex]) {
tmp = data[minIndex];
data[minIndex] = data[nodeIndex];
data[nodeIndex] = tmp;
siftDown(minIndex);
}
}
}
C++ implementation
void BinaryMinHeap::siftDown(int nodeIndex) {
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= heapSize) {
if (leftChildIndex >= heapSize)
return;
else
minIndex = leftChildIndex;
} else {
if (data[leftChildIndex] <= data[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (data[nodeIndex] > data[minIndex]) {
tmp = data[minIndex];
data[minIndex] = data[nodeIndex];
data[nodeIndex] = tmp;
siftDown(minIndex);
}
}
void BinaryMinHeap::removeMin() {
if (isEmpty())
throw string("Heap is empty");
else {
data[0] = data[heapSize - 1];
heapSize--;
if (heapSize > 0)
siftDown(0);
}
}

| Previous: Inserting an element into a heap |
| Next: Building a heap from an array |

Contribute to AlgoList
Liked this tutorial? Please, consider making a donation. Contribute to help us keep sharing free knowledge and write new tutorials.
Every dollar helps!