Looking for hosting? Read HostGator review to find 7 arguments in support of HostGator.

Recursion

Recursion is a technique to divide the problem into subproblems of the same type. Let us see an example.

Calculation of factorial

Factorial of n (denoted n!) is a product of integer numbers from 1 to n. For instance, 5! = 1 * 2 * 3 * 4 * 5 = 120.

Recursion is one of techniques to calculate factorial. Indeed, 5! = 4! * 5. To calculate factorial of n, we should calculate it for (n-1). To calculate factorial of (n-1) algorithm should find (n-2)! and so on. But described process will last infinitely, because no base case has been defined yet. Base case is a condition, when recursion should stop. In the factorial example, a base case is n = 1, for which the result is known.

Java code snippet

This example can be compiled in C++ without modifications.

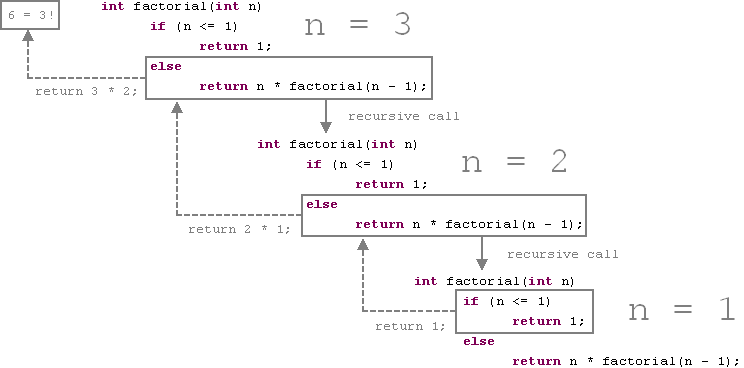
int factorial(int n) {

if (n <= 1)

return 1;

else

return n * factorial(n - 1);

}

Calculation of 3! in details

Advantages and drawbacks of recursion

Main advantage of recursion is programming simplicity. When using recursion, programmer can forget for a while of the whole problem and concentrate on the solution of a current case. Then, returning back to the whole problem, base cases (it's possible to have more than one base case) and entry point for recursion are developed.

On the other hand, recursion has a serious disadvantage of using large amount of memory. Moreover, for most programming languages, recursion use stack to store states of all currently active recursive calls. The size of a stack may be quite large, but limited. Therefore too deep recursion can result in Stack Overflow. To resolve this problem recursion can be simulated, using loop and stack data structure. This approach will be described later.

Partners