Undirected graphs representation
There are several possible ways to represent a graph inside the computer. We will discuss two of them: adjacency matrix and adjacency list.
Adjacency matrix
Each cell aij of an adjacency matrix contains 0, if there is an edge between i-th and j-th vertices, and 1 otherwise. Before discussing the advantages and disadvantages of this kind of representation, let us see an example.
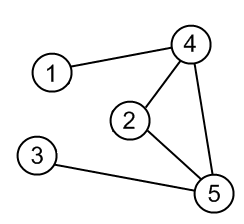 |
 |
| Graph | Adjacency matrix |
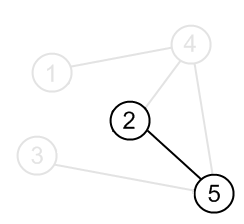 |
 |
| Edge (2, 5) | Cells for the edge (2, 5) |
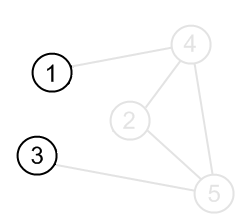 |
 |
| Edge (1, 3) | Cells for the edge (1, 3) |
The graph presented by example is undirected. It means that its adjacency matrix is symmetric. Indeed, in undirected graph, if there is an edge (2, 5) then there is also an edge (5, 2). This is also the reason, why there are two cells for every edge in the sample. Loops, if they are allowed in a graph, correspond to the diagonal elements of an adjacency matrix.
Advantages. Adjacency matrix is very convenient to work with. Add (remove) an edge can be done in O(1) time, the same time is required to check, if there is an edge between two vertices. Also it is very simple to program and in all our graph tutorials we are going to work with this kind of representation.
Disadvantages.
-
Adjacency matrix consumes huge amount of memory for storing big graphs. All graphs can be divided into two categories, sparse and dense graphs. Sparse ones contain not much edges (number of edges is much less, that square of number of vertices, |E| << |V|2). On the other hand, dense graphs contain number of edges comparable with square of number of vertices. Adjacency matrix is optimal for dense graphs, but for sparse ones it is superfluous.
-
Next drawback of the adjacency matrix is that in many algorithms you need to know the edges, adjacent to the current vertex. To draw out such an information from the adjacency matrix you have to scan over the corresponding row, which results in O(|V|) complexity. For the algorithms like DFS or based on it, use of the adjacency matrix results in overall complexity of O(|V|2), while it can be reduced to O(|V| + |E|), when using adjacency list.
-
The last disadvantage, we want to draw you attention to, is that adjacency matrix requires huge efforts for adding/removing a vertex. In case, a graph is used for analysis only, it is not necessary, but if you want to construct fully dynamic structure, using of adjacency matrix make it quite slow for big graphs.
Adjacency list
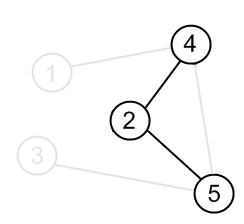
This kind of the graph representation is one of the alternatives to adjacency matrix. It requires less amount of memory and, in particular situations even can outperform adjacency matrix. For every vertex adjacency list stores a list of vertices, which are adjacent to current one. Let us see an example.
 |
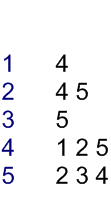 |
| Graph | Adjacency list |
 |
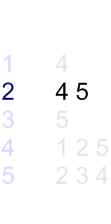 |
| Vertices, adjacent to {2} | Row in the adjacency list |
Advantages. Adjacent list allows us to store graph in more compact form, than adjacency matrix, but the difference decreasing as a graph becomes denser. Next advantage is that adjacent list allows to get the list of adjacent vertices in O(1) time, which is a big advantage for some algorithms.
Disadvantages.
- Adding/removing an edge to/from adjacent list is not so easy as for adjacency matrix. It requires, on the average, O(|E| / |V|) time, which may result in cubical complexity for dense graphs to add all edges.
- Check, if there is an edge between two vertices can be done in O(|E| / |V|) when list of adjacent vertices is unordered or O(log2(|E| / |V|)) when it is sorted. This operation stays quite cheap.
- Adjacent list doesn't allow us to make an efficient implementation, if dynamically change of vertices number is required. Adding new vertex can be done in O(V), but removal results in O(E) complexity.
To sum up, adjacency list is a good solution for sparse graphs and lets us changing number of vertices more efficiently, than if using an adjacent matrix. But still there are better solutions to store fully dynamic graphs.
Code snippets
For reasons of simplicity, we show here code snippets only for adjacency matrix, which is used for our entire graph tutorials. Notice, that it is an implementation for undirected graphs.
Java
public class Graph {
private boolean adjacencyMatrix[][];
private int vertexCount;
public Graph(int vertexCount) {
this.vertexCount = vertexCount;
adjacencyMatrix = new boolean[vertexCount][vertexCount];
}
public void addEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j > 0 && j < vertexCount) {
adjacencyMatrix[i][j] = true;
adjacencyMatrix[j][i] = true;
}
}
public void removeEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j > 0 && j < vertexCount) {
adjacencyMatrix[i][j] = false;
adjacencyMatrix[j][i] = false;
}
}
public boolean isEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j > 0 && j < vertexCount)
return adjacencyMatrix[i][j];
else
return false;
}
}
C++
class Graph {
private:
bool** adjacencyMatrix;
int vertexCount;
public:
Graph(int vertexCount) {
this->vertexCount = vertexCount;
adjacencyMatrix = new bool*[vertexCount];
for (int i = 0; i < vertexCount; i++) {
adjacencyMatrix[i] = new bool[vertexCount];
for (int j = 0; j < vertexCount; j++)
adjacencyMatrix[i][j] = false;
}
}
void addEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j > 0 && j < vertexCount) {
adjacencyMatrix[i][j] = true;
adjacencyMatrix[j][i] = true;
}
}
void removeEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j > 0 && j < vertexCount) {
adjacencyMatrix[i][j] = false;
adjacencyMatrix[j][i] = false;
}
}
bool isEdge(int i, int j) {
if (i >= 0 && i < vertexCount && j > 0 && j < vertexCount)
return adjacencyMatrix[i][j];
else
return false;
}
~Graph() {
for (int i = 0; i < vertexCount; i++)
delete[] adjacencyMatrix[i];
delete[] adjacencyMatrix;
}
};
Recommended books
- Cormen, Leiserson, Rivest. Introduction to algorithms. (Theory)
- Aho, Ullman, Hopcroft. Data Structures and Algorithms. (Theory)
- Robert Lafore. Data Structures and Algorithms in Java. (Practice)
- Mark Allen Weiss. Data Structures and Problem Solving Using C++. (Practice)
Contribute to AlgoList
Liked this tutorial? Please, consider making a donation. Contribute to help us keep sharing free knowledge and write new tutorials.
Every dollar helps!