Binary search tree. Adding a value
Adding a value to BST can be divided into two stages:
- search for a place to put a new element;
- insert the new element to this place.
Search for a place
At this stage analgorithm should follow binary search tree property. If a new value is less, than the current node's value, go to the left subtree, else go to the right subtree. Following this simple rule, the algorithm reaches a node, which has no left or right subtree. By the moment a place for insertion is found, we can say for sure, that a new value has no duplicate in the tree. Initially, a new node has no children, so it is a leaf. Let us see it at the picture. Gray circles indicate possible places for a new node.
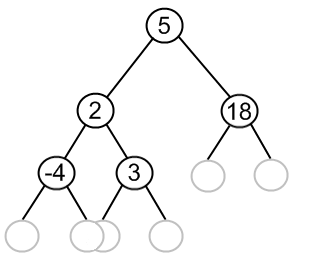
Now, let's go down to algorithm itself. Here and in almost every operation on BST recursion is utilized. Starting from the root,
- check, whether value in current node and a new value are equal. If so, duplicate is found. Otherwise,
- if a new value is less, than the node's value:
- if a current node has no left child, place for insertion has been found;
- otherwise, handle the left child with the same algorithm.
- if a new value is greater, than the node's value:
- if a current node has no right child, place for insertion has been found;
- otherwise, handle the right child with the same algorithm.
Example
Insert 4 to the tree, shown above.

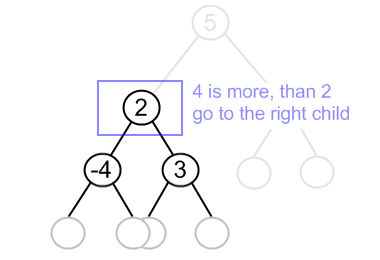
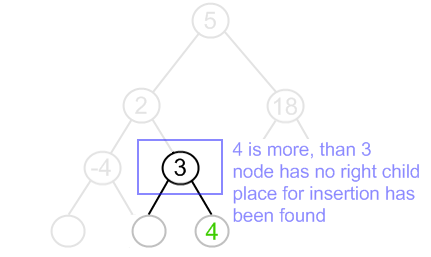
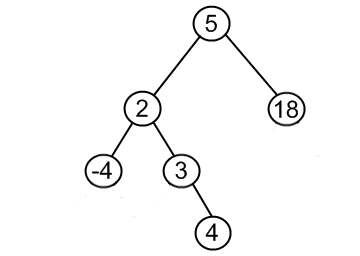
Code snippets
The only the difference, between the algorithm above and the real routine is that first we should check, if a root exists. If not, just create it and don't run a common algorithm for this special case. This can be done in the BinarySearchTree class. Principal algorithm is implemented in the BSTNode class.
Java
public class BinarySearchTree {
…
public boolean add(int value) {
if (root == null) {
root = new BSTNode(value);
return true;
} else
return root.add(value);
}
}
public class BSTNode {
…
public boolean add(int value) {
if (value == this.value)
return false;
else if (value <this.value) {
if (left == null) {
left = new BSTNode(value);
return true;
} else
return left.add(value);
} else if (value > this.value) {
if (right == null) {
right = new BSTNode(value);
return true;
} else
return right.add(value);
}
return false;
}
}
C++
bool BinarySearchTree::add(int value) {
if (root == NULL) {
root = new BSTNode(value);
return true;
} else
return root->add(value);
}
bool BSTNode::add(int value) {
if (value == this->value)
return false;
else if (value < this->value) {
if (left == NULL) {
left = new BSTNode(value);
return true;
} else
return left->add(value);
} else if (value > this->value) {
if (right == NULL) {
right = new BSTNode(value);
return true;
} else
return right->add(value);
}
return false;
}
Visualizers
Recommended books
- Cormen, Leiserson, Rivest. Introduction to algorithms. (Theory)
- Aho, Ullman, Hopcroft. Data Structures and Algorithms. (Theory)
- Robert Lafore. Data Structures and Algorithms in Java. (Practice)
- Mark Allen Weiss. Data Structures and Problem Solving Using C++. (Practice)

| Previous: Internal representation of a BST | Next: Search for a value in BST |

Contribute to AlgoList
Liked this tutorial? Please, consider making a donation. Contribute to help us keep sharing free knowledge and write new tutorials.
Every dollar helps!